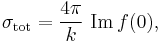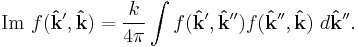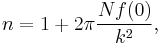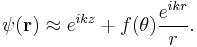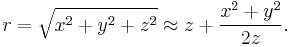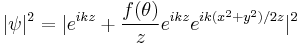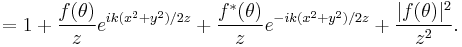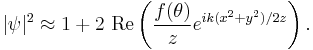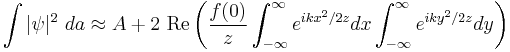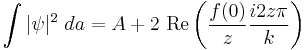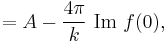Optical theorem
In physics, the optical theorem is a general law of wave scattering theory, which relates the forward scattering amplitude to the total cross section of the scatterer. It is usually written in the form
where f(0) is the scattering amplitude with an angle of zero, that is, the amplitude of the wave scattered to the center of a distant screen. Because the optical theorem is derived using only conservation of energy, or in quantum mechanics from conservation of probability, the optical theorem is widely applicable and, in quantum mechanics,  includes both elastic and inelastic scattering. Note that the above form is for an incident plane wave; a more general form discovered by Werner Heisenberg can be written
includes both elastic and inelastic scattering. Note that the above form is for an incident plane wave; a more general form discovered by Werner Heisenberg can be written
Notice that as a natural consequence of the optical theorem, an object that scatters any light at all ought to have a nonzero forward scattering amplitude, and so a bright central spot.
History
The optical theorem was originally discovered independently by Sellmeier and Lord Rayleigh in 1871. Lord Rayleigh recognized the forward scattering amplitude in terms of the index of refraction as
which he used in a study of the color and polarization of the sky. The equation was later extended to quantum scattering theory by several individuals, and came to be known as the Bohr–Peierls–Placzek relation after a 1939 publication. It was first referred to as the Optical Theorem in print in 1955 by Hans Bethe and Frederic de Hoffmann, after it had been known as a "well known theorem of optics" for some time.
Derivation
The theorem can be derived rather directly from a treatment of a scalar wave. If a plane wave is incident on an object, then the wave amplitude a great distance away from the scatterer is given approximately by
All higher terms, when squared, vanish more quickly than 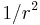 , and so are negligible a great distance away. Notice that for large values of z and small angles the binomial theorem gives us
, and so are negligible a great distance away. Notice that for large values of z and small angles the binomial theorem gives us
We would now like to use the fact that the intensity is proportional to the square of the amplitude  . Approximating the r in the denominator as z, we have
. Approximating the r in the denominator as z, we have
If we drop the 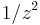 term and use the fact that
term and use the fact that 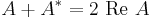 we have
we have
Now suppose we integrate over a screen in the x-y plane, at a distance which is small enough for the small angle approximations to be appropriate, but large enough that we can integrate the intensity from 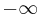 to
to 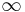 with negligible error. In optics, this is equivalent to including many fringes of the diffraction pattern. To further simplify matters, let's approximate
with negligible error. In optics, this is equivalent to including many fringes of the diffraction pattern. To further simplify matters, let's approximate  . We quickly obtain
. We quickly obtain
where A is the area of the surface integrated over. The exponentials can be treated as Gaussians and so
which is just the probability of reaching the screen if none were scattered, lessened by an amount 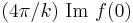 , which is therefore the effective scattering cross section of the scatterer.
, which is therefore the effective scattering cross section of the scatterer.
References
- R. G. Newton (1976). "Optical Theorem and Beyond". Am. J. Phys 44 (7): 639–642. Bibcode 1976AmJPh..44..639N. doi:10.1119/1.10324.
- John David Jackson (1999). Classical Electrodynamics. Hamilton Printing Company. ISBN 0-471-30932-X.